- ホーム
- Databricks
- Databricks-Certified-Professional-Data-Scientist - Databricks Certified Professional Data Scientist Exam
- Databricks.Databricks-Certified-Professional-Data-Scientist.v2022-04-15.q48
- 質問8
有効的なDatabricks-Certified-Professional-Data-Scientist問題集はJPNTest.com提供され、Databricks-Certified-Professional-Data-Scientist試験に合格することに役に立ちます!JPNTest.comは今最新Databricks-Certified-Professional-Data-Scientist試験問題集を提供します。JPNTest.com Databricks-Certified-Professional-Data-Scientist試験問題集はもう更新されました。ここでDatabricks-Certified-Professional-Data-Scientist問題集のテストエンジンを手に入れます。
Databricks-Certified-Professional-Data-Scientist問題集最新版のアクセス
「140問、30% ディスカウント、特別な割引コード:JPNshiken」
同時分布がすでにわかっている2つの確率変数XとYが与えられたとすると、Xの周辺分布は、Yに関する情報を平均したXの確率分布にすぎません。
Yの値がわからない場合のXの確率分布です。では、Xの周辺分布をどのように計算しますか
Yの値がわからない場合のXの確率分布です。では、Xの周辺分布をどのように計算しますか
正解:A,B,C,D
説明
同時分布がわかっている2つの確率変数XとYが与えられた場合、Xの周辺分布は、Yに関する情報を平均したXの確率分布にすぎません。
Yの値がわからない場合のXの確率分布です。これは通常、同時確率分布を合計または統合することによって計算されます。
Y. '離散確率変数の場合、周辺確率質量関数はPr(X = x)と書くことができます。これは、低い信頼度で自動的に生成されたテキストの説明です
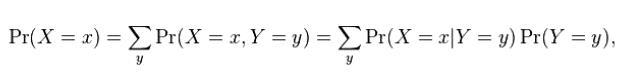
ここで、Pr(X = x、Y = y)はXとYの同時分布であり、Pr(X = x | Y = y)はYが与えられたXの条件付き分布です。この場合、変数Yは無視されています。 。
離散確率変数の2変量周辺確率と同時確率は、多くの場合、双方向テーブルとして表示されます。
同様に、連続確率変数の場合、周辺確率密度関数はpX(x)と書くことができます。これは、中程度の信頼度で自動的に生成された図の説明です
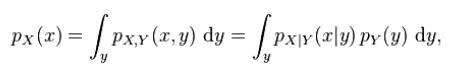
ここで、pX.Y(xy)はXとYの同時分布を示し、pX | Y(x | y)はYが与えられたXの条件付き分布を示します。変数Yは無視されています。
周辺確率は常に期待値として記述できることに注意してください。
テキスト、文字説明は自動的に生成されます
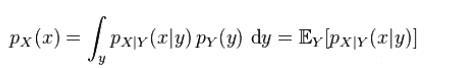
直感的には、Xの周辺確率は、Yの特定の値が与えられた場合のXの条件付き確率を調べ、この条件付き確率をYのすべての値の分布にわたって平均することによって計算されます。図を含む画像説明は自動的に生成されます
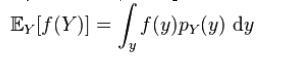
同時分布がわかっている2つの確率変数XとYが与えられた場合、Xの周辺分布は、Yに関する情報を平均したXの確率分布にすぎません。
Yの値がわからない場合のXの確率分布です。これは通常、同時確率分布を合計または統合することによって計算されます。
Y. '離散確率変数の場合、周辺確率質量関数はPr(X = x)と書くことができます。これは、低い信頼度で自動的に生成されたテキストの説明です
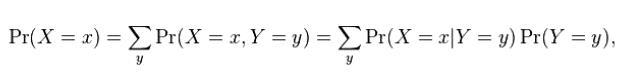
ここで、Pr(X = x、Y = y)はXとYの同時分布であり、Pr(X = x | Y = y)はYが与えられたXの条件付き分布です。この場合、変数Yは無視されています。 。
離散確率変数の2変量周辺確率と同時確率は、多くの場合、双方向テーブルとして表示されます。
同様に、連続確率変数の場合、周辺確率密度関数はpX(x)と書くことができます。これは、中程度の信頼度で自動的に生成された図の説明です
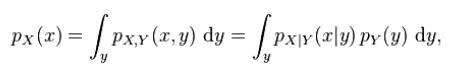
ここで、pX.Y(xy)はXとYの同時分布を示し、pX | Y(x | y)はYが与えられたXの条件付き分布を示します。変数Yは無視されています。
周辺確率は常に期待値として記述できることに注意してください。
テキスト、文字説明は自動的に生成されます
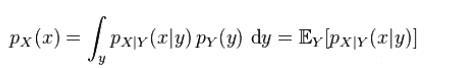
直感的には、Xの周辺確率は、Yの特定の値が与えられた場合のXの条件付き確率を調べ、この条件付き確率をYのすべての値の分布にわたって平均することによって計算されます。図を含む画像説明は自動的に生成されます
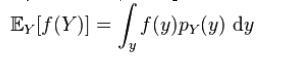
- 質問一覧「48問」
- 質問1 ABC Corpのデータサイエンティストコンサルタントとして、エンド...
- 質問2 質問-18。k-meansアルゴリズムがベクトルのコレクションの適切な...
- 質問3 明示的な分類を与えるのではなく、ある種の報酬システムを使用し
- 質問4 信号機に注意を払わずに横断歩道でヒキガエルを横断しているとき
- 質問5 テストとトレーニングのデータセットはどのライフサイクルステー
- 質問6 分類子モデルを構築するためにデータを分析しています。モデルに
- 質問7 データを多くの機能から少数に減らして、2次元または3次元で適切...
- 質問8 同時分布がすでにわかっている2つの確率変数XとYが与えられたと...
- 質問9 あなたは母集団の行動を研究しており、個人レベルで多次元データ
- 質問10 別紙を参照 (Exhibit) 展示では、x軸は、借り手がローンをデフォ...
- 質問11 特定の雑誌の月間購読者の総数を予測するモデルを作成するように
- 質問12 教師あり学習の例はどれですか?
- 質問13 分類と回帰は___________の例です。
- 質問14 線形回帰モデルを使用できるシナリオはどれですか?
- 質問15 質問-26。5000種類のカラーボールがあり、そのうち1200色はピン...
- 質問16 特定の食料品店から購入した10,000人のデータがあります。また、...
- 質問17 教師あり学習に適用される正しいステートメントを選択してくださ
- 質問18 次のうち、分類の正しいアプリケーションではないものはどれです
- 質問19 最初のサイコロが6であるとすると、2つのサイコロの合計が8より...
- 質問20 単純ベイズ分類に関する正しいステートメントを選択してください
- 質問21 E1とE2が2つのイベントである場合、E1が発生した場合にE2が発生...
- 質問22 映画のレイティングについて、以下の2つのケースがあるとします
- 質問23 K-Meansクラスタリングアルゴリズムに関して正しいのは次のうち...
- 質問24 果物が赤く、丸く、直径が約3インチの場合、果物はリンゴと見な
- 質問25 すべての機能の中で独立性を前提としている分類器を見つけますか
- 質問26 レコメンダーシステムの設計に使用できる手法は次のうちどれです
- 質問27 以下の問題ステートメントを解決するためにどのテクニックを使用
- 質問28 データサイエンティストは、年齢、性別、血中コレステロール値の
- 質問29 開発中の機械学習アプリケーションのシーケンスを選択します A)...
- 質問30 回帰モデルの決定係数値について正しい説明は次のうちどれですか
- 質問31 レコメンダーシステムを設計および評価しているeコマース組織で
- 質問32 ロジスティック回帰法の真の制限を説明するものは何ですか?
- 質問33 回帰(教師あり学習)のターゲット変数の正しい例は次のうちどれ
- 質問34 回帰アルゴリズムが最適ではない選択肢を選択してください
- 質問35 展示を参照してください。 (Exhibit) 大規模小売業者の顧客行動...
- 質問36 研究者は、GRE(Graduate Record Examスコア)、GPA(成績平均)...
- 質問37 1〜5つ星の評価システムのモデルを作成したとします。そして、RM...
- 質問38 主成分分析(PCA)に基づく方法では、次のように特徴を評価しま...
- 質問39 頭の確率がpであるコインを裏返すことを検討してください。ここ
- 質問40 A、B、およびCがイベントであるとします。P(| C)に対するAのB...
- 質問41 次の指標のうち、レコメンダーシステムの精度と品質を測定するの
- 質問42 あなたの会社は、製品の品質に関するフィードバックのためのオン
- 質問43 正則化は、過剰適合を防ぐための機械学習において非常に重要な手
- 質問44 マリーは明日、砂漠での野外式典で結婚します。近年、雨は毎年5
- 質問45 次のシナリオのどれで、分類にnaTveベイズの定理を使用できます...
- 質問46 L1とL2の正則化の大きな違いは何ですか?
- 質問47 電子メールのスパムフィルタリングは、
- 質問48 質問-34。ストーリーは、コミュニティによって「投票」(肯定的...

[×]
Download PDF File
Enter your email address to download Databricks.Databricks-Certified-Professional-Data-Scientist.v2022-04-15.q48.pdf
