- ホーム
- CompTIA
- DA0-001J - CompTIA Data+ Certification Exam (DA0-001日本語版)
- CompTIA.DA0-001J.v2025-02-04.q133
- 質問107
有効的なDA0-001J問題集はJPNTest.com提供され、DA0-001J試験に合格することに役に立ちます!JPNTest.comは今最新DA0-001J試験問題集を提供します。JPNTest.com DA0-001J試験問題集はもう更新されました。ここでDA0-001J問題集のテストエンジンを手に入れます。
DA0-001J問題集最新版のアクセス
「365問、30% ディスカウント、特別な割引コード:JPNshiken」
ランディは数学のテストで 76 点、ケイティは科学のテストで 86 点、ラルフは歴史のテストで 80 点、ジーンは英語のテストで 80 点を獲得しました。以下の表には、各コースのスコアの平均と標準偏差が含まれています。
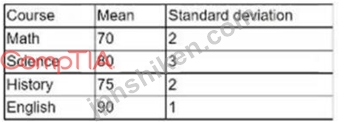
この情報を使用して、次の生徒のうち誰が最高のスコアを獲得しましたか?

この情報を使用して、次の生徒のうち誰が最高のスコアを獲得しましたか?
正解:B
To compare the students' scores, we need to standardize them by using the z-score formula, which is:
z = (x - #) / #
where x is the raw score, # is the mean, and # is the standard deviation. The z-score tells us how many standard deviations a score is above or below the mean. A higher z-score means a better score relative to the average.
Using the table, we can calculate the z-scores for each student as follows:
Randy: z = (76 - 70) / 2 = 3 Katie: z = (86 - 80) / 3 = 2 Ralph: z = (80 - 75) / 2 = 2.5 Jean: z = (80 - 90) / 1 =
-10
The student with the highest z-score is Randy, with a z-score of 3. This means that Randy scored 3 standard deviations above the mean in math, which is the best performance among the four students. Therefore, the correct answer is A.
References: Comparing with z-scores (video) | Z-scores | Khan Academy, 17 Important Data Visualization Techniques | HBS Online
z = (x - #) / #
where x is the raw score, # is the mean, and # is the standard deviation. The z-score tells us how many standard deviations a score is above or below the mean. A higher z-score means a better score relative to the average.
Using the table, we can calculate the z-scores for each student as follows:
Randy: z = (76 - 70) / 2 = 3 Katie: z = (86 - 80) / 3 = 2 Ralph: z = (80 - 75) / 2 = 2.5 Jean: z = (80 - 90) / 1 =
-10
The student with the highest z-score is Randy, with a z-score of 3. This means that Randy scored 3 standard deviations above the mean in math, which is the best performance among the four students. Therefore, the correct answer is A.
References: Comparing with z-scores (video) | Z-scores | Khan Academy, 17 Important Data Visualization Techniques | HBS Online
- 質問一覧「133問」
- 質問1 アナリストは、さまざまなソースからデータを抽出し、クリーニン
- 質問2 ACME Corporation は、Excel ドキュメントのデータ品質の問題を...
- 質問3 以下の画像を考えてみます。 (Exhibit) 次のファイル形式のうち...
- 質問4 既知のパターンが破られている場合、または新しいパターンが出現
- 質問5 離散データと連続データの違いを最もよく説明しているものは次の
- 質問6 分析前に 2 つ以上のグループに分類する必要がある変数を扱う場...
- 質問7 アナリストは、組織が過去 6 年間にサービスを提供した顧客数に...
- 質問8 アナリストは気象データを含むレポートを作成しています。温度は
- 質問9 データ プロファイリング中に、アナリストは次のデータ セットの...
- 質問10 PII の例は次のうちどれですか?
- 質問11 回収マネージャーには、支払い期限を過ぎた顧客に電話して支払い
- 質問12 アナリストがビジネス上の質問のレビューを実施しました。分析を
- 質問13 暗号化は、データを保護するためのメカニズムです。 いつデータ
- 質問14 5 匹の犬の身長は次のミリメートルです。 300、430、170、470、6...
- 質問15 次のレポートを参考にしてください。 (Exhibit) レポートが特定...
- 質問16 アナリストは、プライマリ アカウント番号、有効期限、サービス ...
- 質問17 調査データを確認しているときに、調査アナリストは、1 つの質問...
- 質問18 11 人の退職年齢を示すこのデータセットを考慮してください。 54...
- 質問19 新しいツールを入手することを意味する場合でも、特定の状況に最
- 質問20 メイン リポジトリからの代表的な量のデータの使用について説明
- 質問21 レポートアナリストは、営業組織の前年比パフォーマンスを示すダ
- 質問22 シリアル製造業者は、シリアルの糖度が長年にわたって増加してい
- 質問23 マリオは、会計システムからデータ ウェアハウスへのデータのコ
- 質問24 データ サイエンティストは、どの製品が最も収益を上げ、どの製
- 質問25 次の統計手法のうち、2 つ以上のカテゴリ変数が必要なのはどれで...
- 質問26 月ごとの売上のデータ セットには、次のデータが含まれます。 (E...
- 質問27 データ操作を伴ってあるデータベースから別のデータベースにデー
- 質問28 次のデータ保護方法のうち、転送中のデータの機密性を保証するも
- 質問29 最高経営責任者 (CEO) は、月末前に可視性を高めるために、より...
- 質問30 次のことを前提とします。 (Exhibit) トレンド分析のためにテー...
- 質問31 あるビジネス ユニットがテーブル内の値に次の変更を加えました
- 質問32 データ アナリストは、各従業員の名、姓、売上、住所を含む 1 つ...
- 質問33 リレーショナル データベース内に格納されている情報を追加、削
- 質問34 インタラクティブな視覚化とビジネス機能、およびエンド ユーザ
- 質問35 データ セットのデータを最もよく要約するためにアナリストが行
- 質問36 アナリストは、個人のファーストネームとラストネームを別々の列
- 質問37 Jhon は、6 つの異なるソース システムからデータを調達する ELT...
- 質問38 最小限のストレージデータを使用して顧客の年齢を保存するのに最
- 質問39 データ アナリストは、2020 年第 2 四半期の取締役会向けの売上...
- 質問40 次のうち、一般的なデータ ウェアハウス スキーマはどれですか?...
- 質問41 以下の表をご覧ください。 (Exhibit) 次の変数タイプのうち、「...
- 質問42 データ アナリストは、販売のストーリーを提供し、顧客ごとの販
- 質問43 アナリストは毎日レポートを実行し、データを分析する前にデータ
- 質問44 最近、e コマース企業が新しい Web サイトのレイアウトをテスト...
- 質問45 アナリストは、次のデータセットを使用して、2022 年のシカゴの...
- 質問46 従来のデータ ソースを更新する場合のベスト プラクティスは次の...
- 質問47 企業の上級管理チームは、各四半期の終わりに詳細な販売レポート
- 質問48 データベース管理者は、承認されたユーザーのみが特定のデータベ
- 質問49 アナリストは、売上と売上顧客比率のストーリーを提供するダッシ
- 質問50 Amanda は、他の多くのデータ ソースから情報を引き出してビジネ...
- 質問51 次のデータ テーブルがあるとします。 (Exhibit) 次の MDM プロ...
- 質問52 次のプログラミング言語のうち、分析アプリケーションで使用する
- 質問53 アナリストは迅速な分析を行う必要があります。アナリストがデー
- 質問54 データ アナリストは、さまざまな地域、製品、および期間に関す
- 質問55 ユーザーは毎日データ ファイルを買掛金システムにインポートし
- 質問56 次のどれに英数字の値が含まれていますか?
- 質問57 タブ区切りの spre ファイルとして正しいのはどれですか?
- 質問58 データベースは、複数のディメンションで構成される 1 つのファ...
- 質問59 データ アナリストは、順次導入されるプラスまたはマイナスの値
- 質問60 次のデータテーブルがあるとします。 (Exhibit) データ クレンジ...
- 質問61 データ アナリストは、差異が大きいため、データ セットから外れ...
- 質問62 アナリストは、米国の郊外の家族の収入データを扱っています。デ
- 質問63 データセットはマルチメディア技術を使用して記録されました。解
- 質問64 2020 年 4 月 9 日の朝、データ アナリストは、年初来の売上高を...
- 質問65 アナリストは、デジタル ニュース アウトレットの記事で見つかっ...
- 質問66 現在の日付は 2020 年 7 月 14 日です。データ アナリストは、同...
- 質問67 次の値のうち、降順に並べ替えた場合に最初に表示されるのはどれ
- 質問68 アナリストは、従業員イントラネット サイトの分析ダッシュボー
- 質問69 次のうち、データ侵害を防止するための管理手段はどれですか?
- 質問70 通常、要約統計量と見なされないものは次のうちどれですか?
- 質問71 顧客アンケートでは 90% が肯定的なフィードバックを示していま...
- 質問72 データの統計と情報を調べるプロセスを最もよく説明しているのは
- 質問73 次のうち、一般的なデータ統合ツールではないものはどれですか?
- 質問74 データの定量化に使用される手法は次のうちどれですか?
- 質問75 財務アナリストは、会社の日次請求レポートを作成しています。あ
- 質問76 データ アナリストは、以下の表を次の方法で整理するように依頼
- 質問77 ジョセフは、左に歪んだテスト スコアの分布を解釈しています。
- 質問78 データマイニング ETL ツールの例は次のうちどれですか?
- 質問79 あるアナリストが、2019 年の最初の 2 四半期で売り上げが $50,0...
- 質問80 調査アナリストは、分析対象のデータが他のデータポイントに接続
- 質問81 組織が目標をどの程度達成しているかを測定したいと考えています
- 質問82 アナリストは毎月、過去 2 か月分のデータを取得する必要があり...
- 質問83 次のうち、離散変数の例はどれですか?
- 質問84 次のうち、離散データ型の例はどれですか?
- 質問85 ノンパラメトリック検定は次のうちどれですか?
- 質問86 'テーブルの代わりにデータベース ビューを使用する最も良い理由...
- 質問87 データ アナリストは、毎日生産される石油のガロン数を示す一連
- 質問88 フラット テキスト ファイルと他のデータ タイプの違いは次のう...
- 質問89 コールセンターが 1 日に受ける電話の数は次の例です。
- 質問90 データ アナリストは、正確性を保つために、データ セットに品質...
- 質問91 重線形回帰モデルの作成に最適なテクノロジーは次のうちどれです
- 質問92 データ アナリストは、以下のデータ セットを使用して第 1 四半...
- 質問93 次のデータ型のうち、4Ac1 を最もよく表すのはどれですか? (2 つ...
- 質問94 Andy は小売業者の価格アナリストです。彼は仮説検定を使用して...
- 質問95 データ エンジニアは、顧客がバニラ アイスクリームを好むかどう...
- 質問96 次のうち、計算とピボット テーブルに使用されるものはどれです
- 質問97 アナリストは、新規顧客の割合が最も高いサイトを判断するための
- 質問98 今月の収益レポートの合計値は先月の 2 倍です。ETL プロセス中...
- 質問99 データ アナリストは、以下の表のデータ セットを使用して、各生...
- 質問100 アナリストは、調査回答データ セットのカテゴリ間の構成を特定
- 質問101 次のうち、データ統合中にデータを収集、ブレンド、およびロード
- 質問102 アナリストはユーザー用に新しいダッシュボードを構築しています
- 質問103 次のうち、テキストの正しいデータ型はどれですか?
- 質問104 次の顧客テーブルと注文テーブルがあるとします。 次のうち、テ
- 質問105 正規化されたディメンション テーブルを特徴とするデータベース ...
- 質問106 病院データベースのテーブルには、患者の身長 (インチ) の列と患...
- 質問107 ランディは数学のテストで 76 点、ケイティは科学のテストで 86 ...
- 質問108 ユーザーは、さまざまな日付範囲で会社の売上を追跡するための大
- 質問109 データアナリストはチームと協力して、オンデマンド アクセスを
- 質問110 統計ソフトウェア内で探索的分析を開始するのに最適なファイル形
- 質問111 Microsoft が提供し、SQL Server データベースと直接統合される...
- 質問112 データ分析レポートのビジネス要件を理解した後、次に達成する必
- 質問113 以下のことを考えると: (Exhibit) 次の数字のうち、タイプ I エ...
- 質問114 以下の図を考えてみます。 (Exhibit) 次の手順のうちどれが不足...
- 質問115 探索的分析を最もよく表すものは次のうちどれですか?
- 質問116 アナリストは、特定の日付に基づいて特定のレコードを選択する際
- 質問117 アンジェラは、従業員システムのデータを使用して CRM システム...
- 質問118 アナリストは、新規顧客の調査から得た情報を使用して、顧客連絡
- 質問119 公開グループは、公開前に投稿を追跡するためのダッシュボードを
- 質問120 営業マネージャーは、四半期ごとの販売レポートをユニットおよび
- 質問121 営業ディレクターが、部門内の個々のチーム メンバー向けのレポ
- 質問122 ダニエルは、構造化クエリ言語を使用して、リレーショナル デー
- 質問123 開発会社がアパートの複合施設内に新しい Init を建設しています...
- 質問124 次のうち、データの要素が母集団内の小さなサブグループのそれぞ
- 質問125 データ アナリストは、以下の表を使用してスプレッドシート内で
- 質問126 次のうち、フラット ファイルの例はどれですか?
- 質問127 次の変数名形式のうち、大部分のデータ ソフトウェア プログラム...
- 質問128 研究アナリストは 1,000 個の標本から 10 個のデータ ポイントを...
- 質問129 展示する。 (Exhibit) 次の論理ステートメントのうち、表 B の結...
- 質問130 金融サービス会社の顧客リストを以下に示します。 (Exhibit) デ...
- 質問131 若い Web 開発者が、ユーザーが短い動画をアップロードできる新...
- 質問132 調査データを確認しているときに、アナリストは、回答者が 1 月...
- 質問133 データ アナリストは、次の情報に基づいて小売店が顧客を 5 つの...

